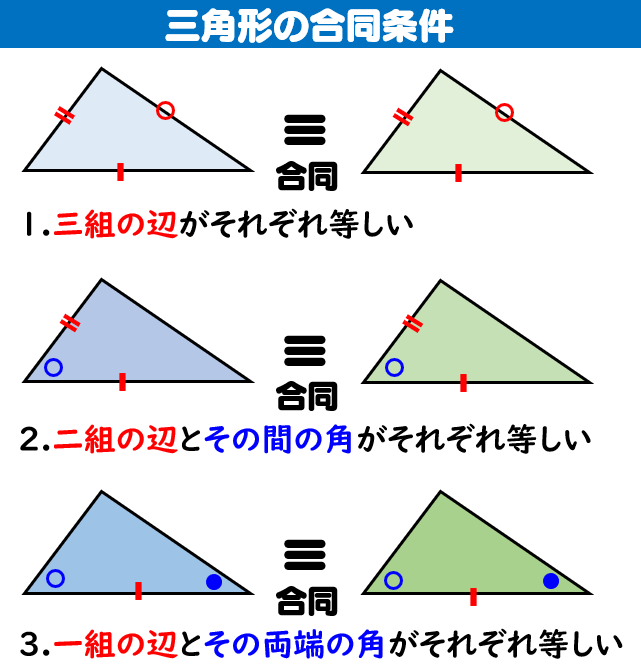
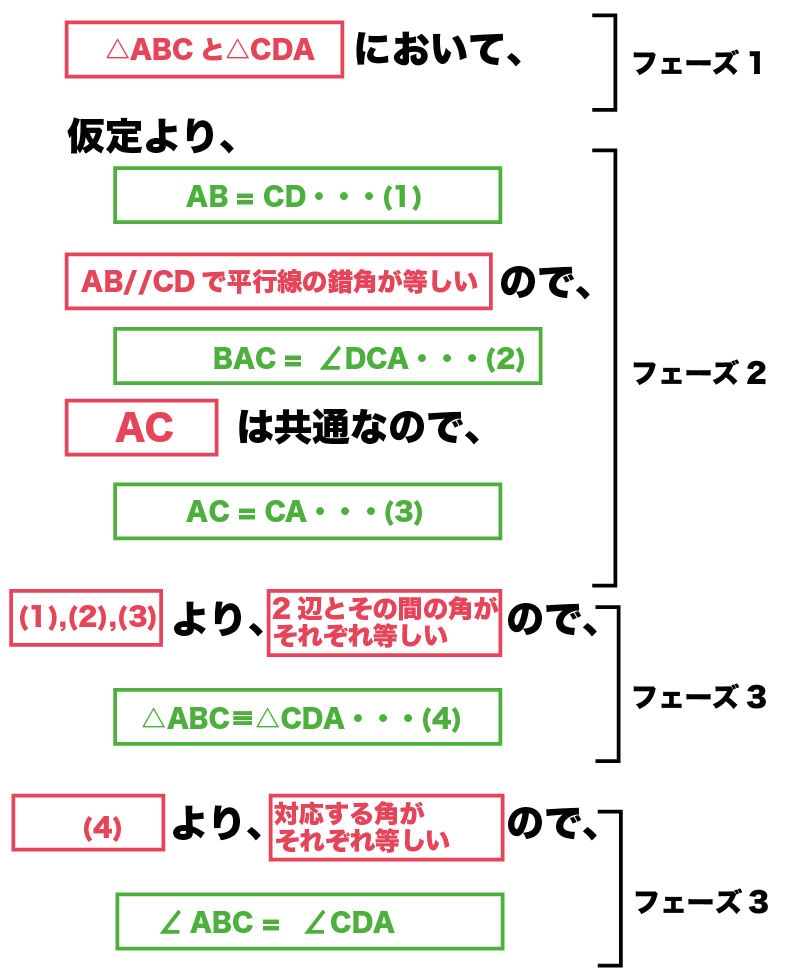
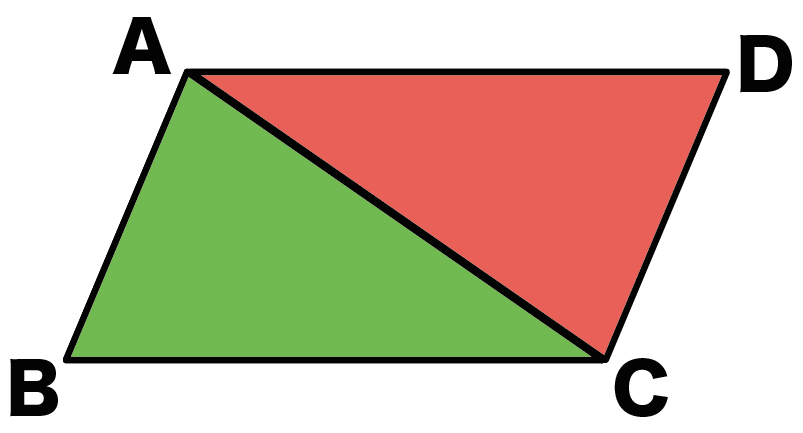
合同な表し方 三角形の合同条件 合同な図形を選ぶ練習 証明のしくみ 仮定と結論 証明の進め方 1結論(=ゴール、目的)を確認する 2結論を達成するにはどうしたらいいか、その方法を考える 合同の証明練習問題三角形の合同証明3(角の共通) 共通の角 図の∠aは abdの角であると同時に aceの角でもある。 このような角を 共通 という。 証明では「∠aは共通」または「∠bad=∠cae(共通)」三角形の合同の証明① 下の図で,ab=ac,−bad=−cad である。このとき,¼abd×¼acd で あることを右のように証明した。下線部 をうめて,証明を完成させなさい。 三角形の合同の証明② 下の図で,am=cm,bm=dm であ る。このとき,ab=cd であることを右

中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath
三角形 合同 証明 書き方
三角形 合同 証明 書き方- 三角形の合同証明の総合的な練習問題です。定期テスト対策や高校入試対策としてもご利用ください。三角形の合同証明のポイント基本的な合同条件、証明のやり方をしっかり確認してから取り組んでください。 三角形の合同 二等辺三角形 直角三角形1合同なることを証明する三角形を囲んで証明問題の解き方の流れ ここからは証明問題の解き方の流れを具体的に解説します。 証明するための条件選び 合同の証明には以下3パターンの条件のいずれかを用います。 三組の辺がそれぞれ等しい;




中2数学 証明はハンバーガーだ2 中身の書き方のコツ 練習編 映像授業のtry It トライイット
二等辺三角形の証明のまとめ ・(証明以外で)二等辺三角形がある時 底角が等しいことを使う 頂角の二等分線を引く→底辺を垂直に二等分する 90°ができる 底辺との交点が、底辺の中点となる ・二等辺三角形の証明 合同な三角形でなく角を利用 今回は、長さ の辺を選び、これを底辺としましょう。 STEP2 底辺の両端からほか 2 辺の長さの弧を描く コンパスと定規を使って、残りの 辺を書きましょう。 まず、コンパスの幅(半径)を にとって底辺の一端にコンパスの針をおき、弧を つ描きます。 同様に、今度はコンパスの幅(半径)を にとって底辺のもう一端から弧を つ描きます。 それらの弧 三角比6|正弦定理の使い方を具体例から考えよう 三角比を学ぶことで正弦定理と余弦定理という三角形に関する非常に便利な定理を証明することができます. だということは容易に想像が付きますね( 余弦定理 は次の記事で扱います
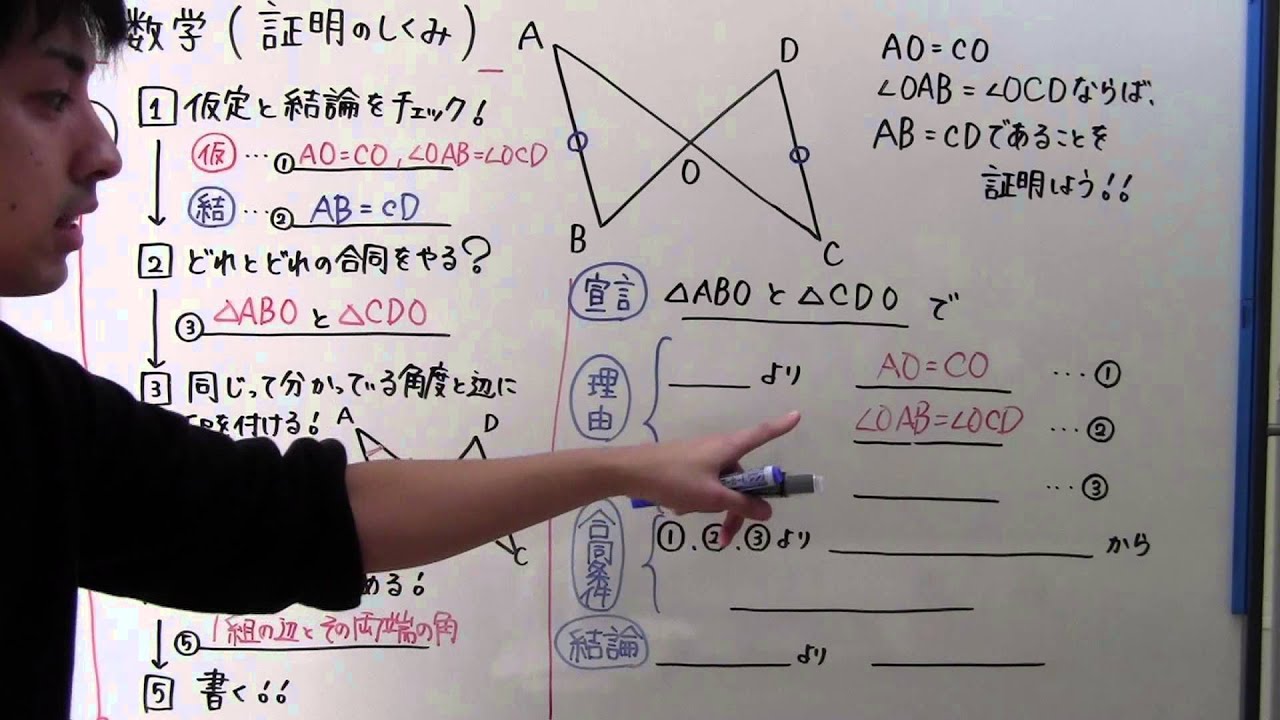
前回は「直角三角形の合同条件」を学習しました 今回は「直角三角形の合同」を利用して「等式を証明する問題」等を一緒に見ていきましょう ホーム; 長辺が中心Oを通る三角形A'BCは∠Bを90°とする直角三角形になる。 よって、 $$\sin A' = \frac{ a }{ 2R }$$ 整理すると $$\frac{ a }{ \sin A' } = 2R$$ 円周角の定理より、∠A'=∠Aであるから、 $$\frac{ a }{ \sin A } = 2R①$$ 正弦定理の証明:2 Aが直角(90°)のとき証明の手順 1.仮定を探して書く ↓ 2. 仮定以外 で同じ大きさのものを書く ↓ 3. 「三角形の合同条件」 の3つのうち、どれかを書く ↓ 4.結論を書く証明はこの手順で進めるものです。 "2と3の部分" で、 苦戦する中学生が多いですね。
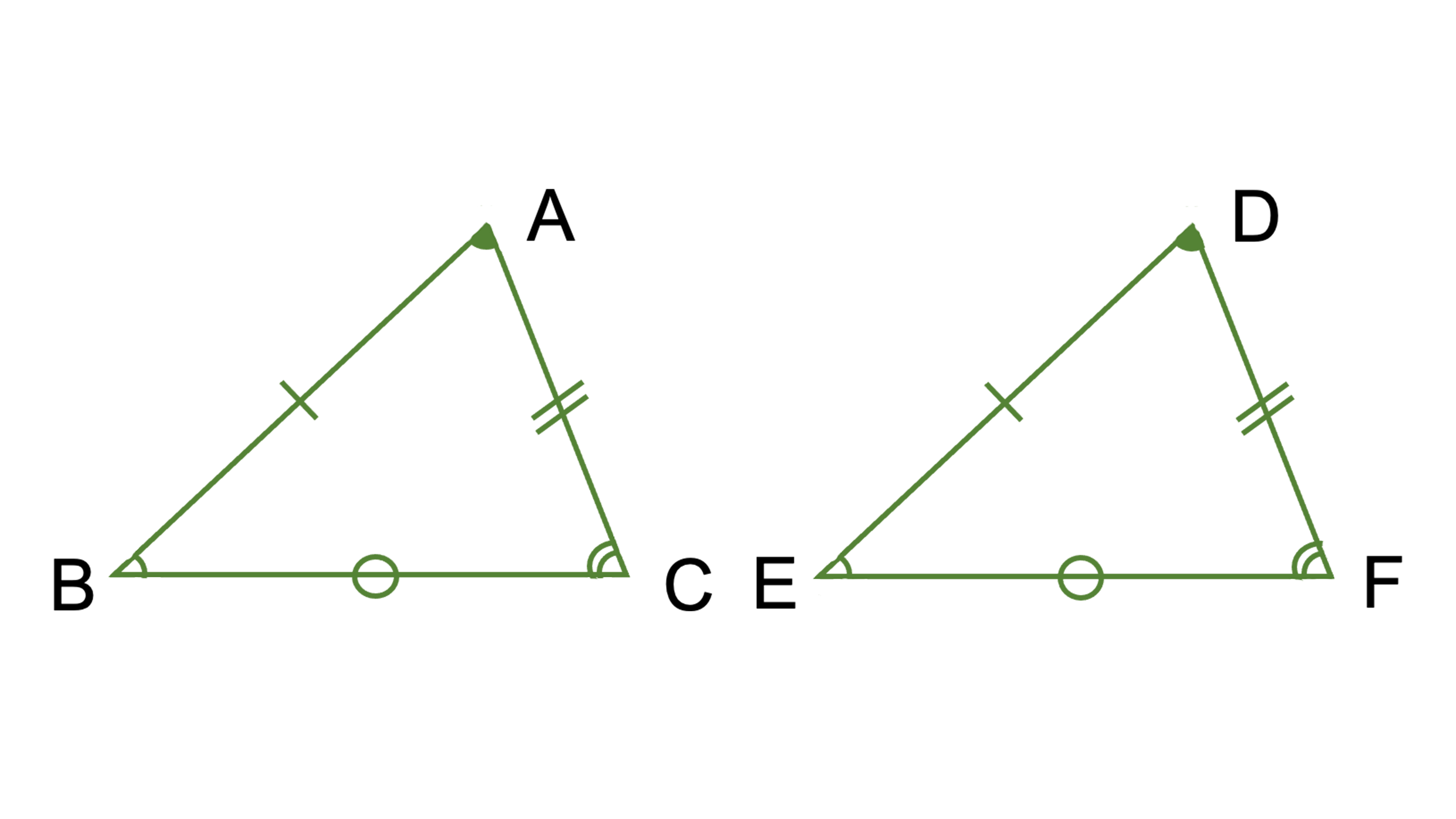
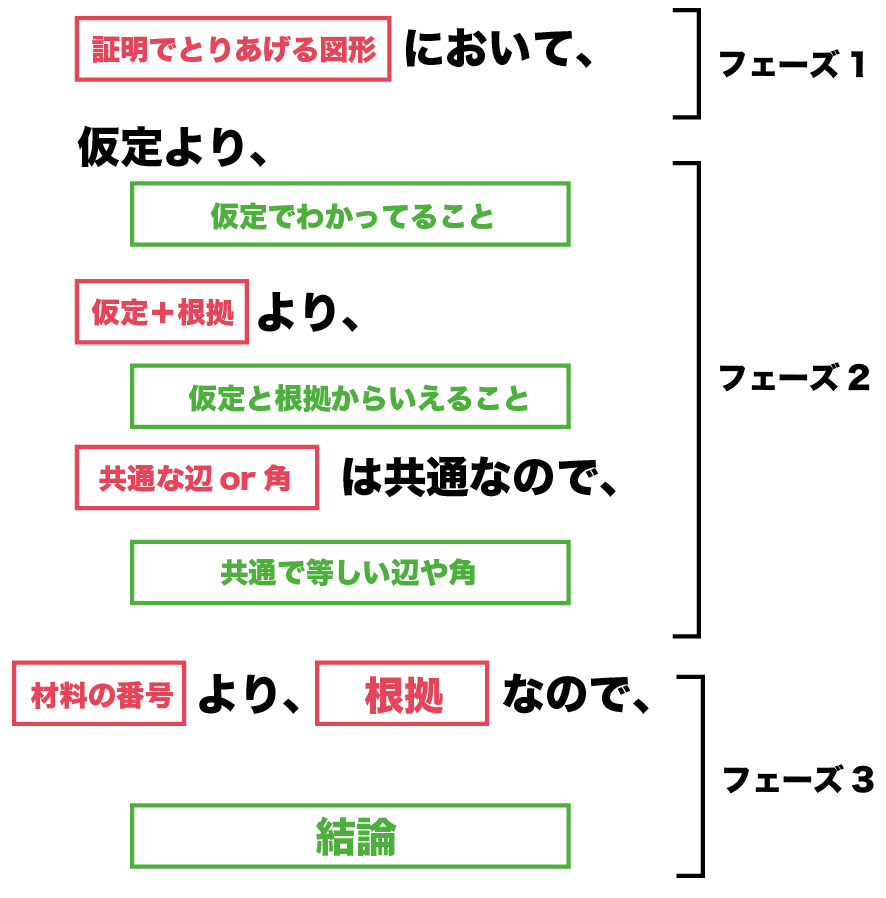
証明の流れ <合同な三角形を証明する場合> ( )と ( )において ( )=( )(根拠・理由)① ( )=( )(根拠・理由)② ( )=( )(根拠・理由)③ ①②③より( 合同条件 )より ( )≡ ( ) 三角形の合同条件 三角形の証明問題で「 ABCと PQRで・・・」と書き始めたとき、おのおのの辺と角の表し方には基本形があるのでしょうか?手元の問題集や教科書では「AB=PQ、BC=QR、AC=PR、∠ABC=∠PQR 数学 解決済 教えて!goo 三角形の書き方(作図) いろいろな三角形の作図方法については、以下の記事で説明しています。 正三角形・二等辺三角形・直角三角形の書き方(作図)まとめ! 以上で、解説を終わります。 三角形についてたくさんのことを解説していきましたが、理解




数学の証明問題について 証明の書き方についてアドバイスを頂けないで 数学 教えて Goo
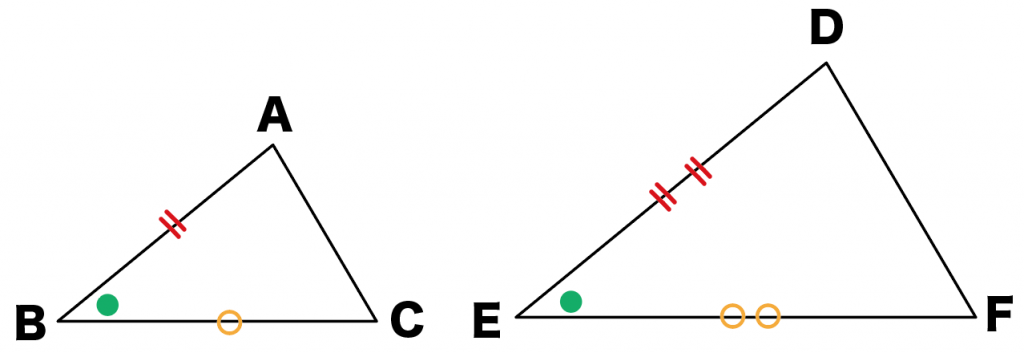



中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
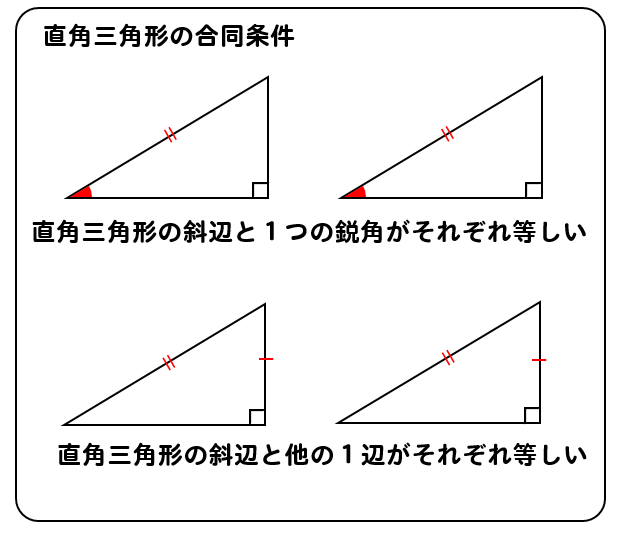
こんにちは、ウチダです。 今日は、中学2年生で習う 「直角三角形の合同条件」 について、まず「そもそもなぜ成り立つのか」を考察し、次に直角三角形の合同条件を使った証明問題を解説していきます。 直角三角形の合同条件2つ まず、一般的な三角形における合同条件3つについて、理解 証明の締め方ですが、学校のテストなら習った通りの書き方でやるのが一番いいと思います。無難にやるなら「(証明終)」、他には「 」「//」何かもありますね。 三角形の証明問題を見てみよう 実際に問題を出しつつ、自分なりの考え方を紹介します。直角三角形の問題もやってみましょう。合同 の 証明 合同の証明 書き方 数学4.平面図形 3.合同の証明 複合問題ほか 02年度 数学4.平面図形 3.合同の証明 複合問題ほか 03年度 数学4.平面図形 3.合同の証明 複合問題ほか 05年度 数学4.平面図形 3.合同の証明 複合問題ほか 07年度中学2年生 数学 合同と証明 練習問題プリント



1




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張
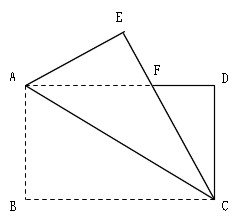
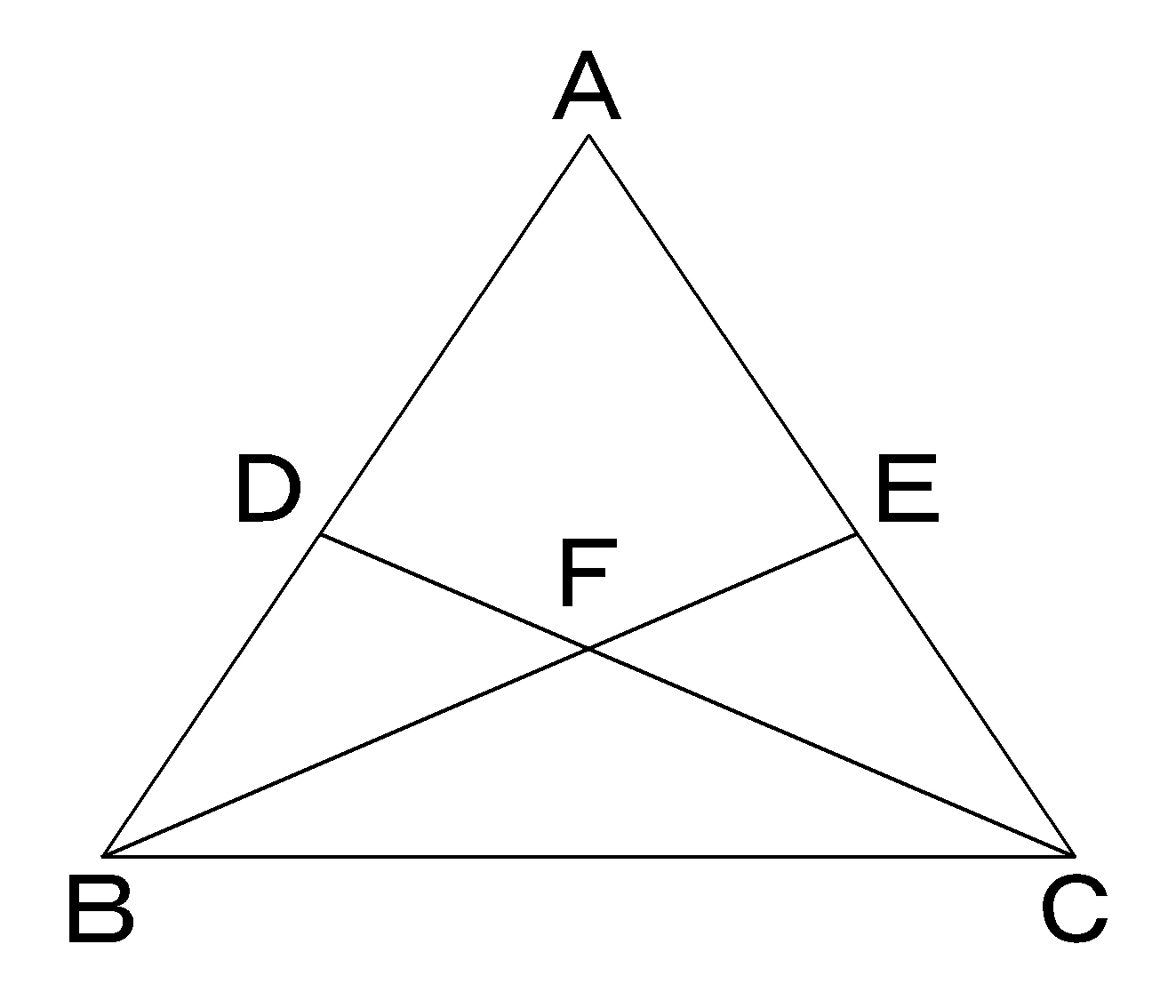
証明2:三角形の面積を用いる方法(エレガント,中学生でも理解できる) 証明3: d d d を点 A A A の関数と見る方法(珍しい発想,やや難しい) 目次 ベクトルを用いた距離公式の証明 三角形の面積を用いた距離公式の証明 おまけにもう1つ距離公式の証明 ベクトルを用いた距離公式の証明 よって、 opaはop = oaの二等辺三角形である。 二等辺三角形の底角は等しいから、 ∠oap = ∠opa ・・・ (1) 三角形の外角の定理より、 ∠aoq = ∠oap ∠opa・・・(2) (1)、(2)より、 ∠apq = 1/2∠aoq・・・(3)(1) 三角形 CBF は二等辺三角形であることを証明せよ。 (2) AB=10 cm , AC=8 cm とするとき,次の①・②の問いに答えよ。 ① 線分 AE の長さを求めよ。 ② 線分 DE の長さを求めよ。




この証明の書き方を教えてください Clear
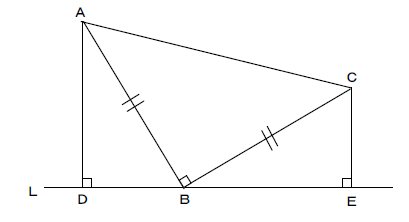



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 Atstudier
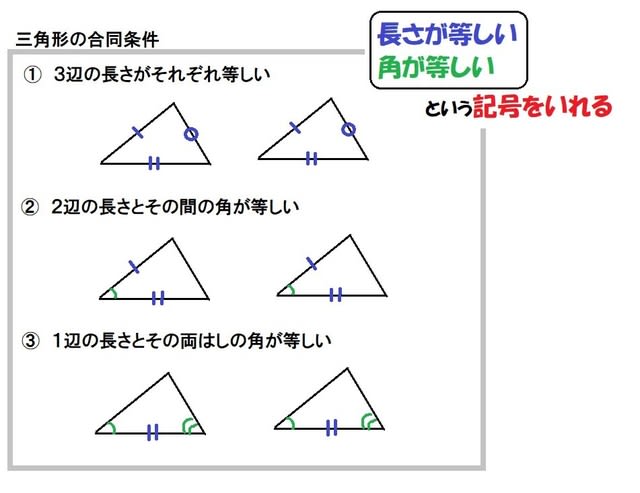
三角形の合同の証明の書き方 基本的な書き方 三角形の合同の証明を書くときは基本的には以下の手順で書いていきます。 まずどの三角形の合同を証明するか明示する。 次に証明に必要な「角度の一致」、「辺の長さの一致」を書く。 どの合同条件を使用したかを書く。三角形の合同証明の進め方中2数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・三角形の合同証明の、進める手順に慣れよう 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 327K subscribersここでは解答の流れと書き方だけ簡単に説明しておきます。 合同を証明したい2つの三角形を書きます。 \(\,\mathrm{ ABC}\,\)と\(\,\mathrm{ DEF}\,\)において ここから示していくのは合同条件をいうために必要な条件です。 三角形の合同条件は5つあります。



正三角形と証明 中学2年 数学クラブ




中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
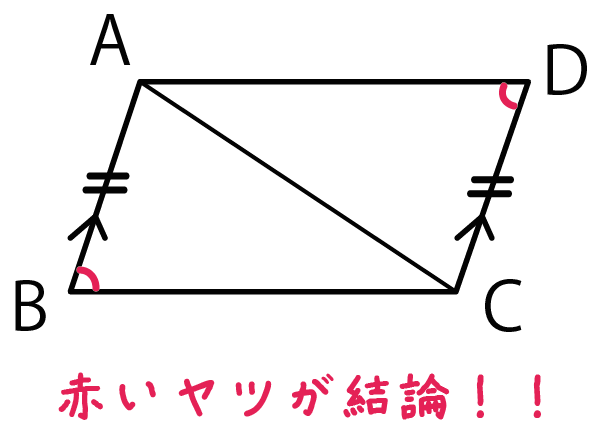
もう一つのコツは、 分かったことを図に書きこんでいくこと。 合同証明の問題文には「仮定」が書いてあります。 仮定でわかったことを図に書き込んでいきましょう。 正三角形ならば、三辺が等しいのも仮定です。 AB=CDという仮定を見つけたら、辺上に「〃」のマークを付けるなどします。 正三角形なら、3つの角が60度で等しいですね。 ∠ABC=∠DEFを見つけ 2 数学三角形の内接円の書き方:コンパスを使った角の二等分線の作図がポイント 3 数学での内心が1つに定まる背景:三角形の二等分線が一点で交わることの証明 4 円の接線が90°なのは本当なのか? 5 まとめ 三角形の内心とは? 数学での意味を、多角形とは・内接の意味を含めて解説 世間一般では心のうちを意味する言葉として「内心怖かった 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは




この証明の書き方がわからないので教えてください 発展の1はあっているか答え合わ Clear




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath
直角三角形なので左下の角度は90°θとなります。 左下の角度で三角比を取ると、 sin(90° −θ) = x r sin ( 90 ° − θ) = x r となりますよね。 見たことのある形になりました。 そうです、これは cosθ = x r cos辺=辺 ① 辺=辺 ② 辺=辺 ③ また、三角形に必ず外接円(外側に接している円)が存在する理由は、数学a「図形の性質」で "外心" を習うときに学びます。 ⇒参考「外心とは?三角形の外心の座標・位置ベクトルの求め方や性質の証明をわかりやすく解説!垂心」




証明の書き方で最初に と において と書く時 Clear



Q Tbn And9gcs8jzs Zkdiyrmuisoi0mwqzez E9r9gwygbti5ixce9rlyfs0 Usqp Cau
中2数学 中2数学「直角三角形の証明」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21年8月31日 / 21
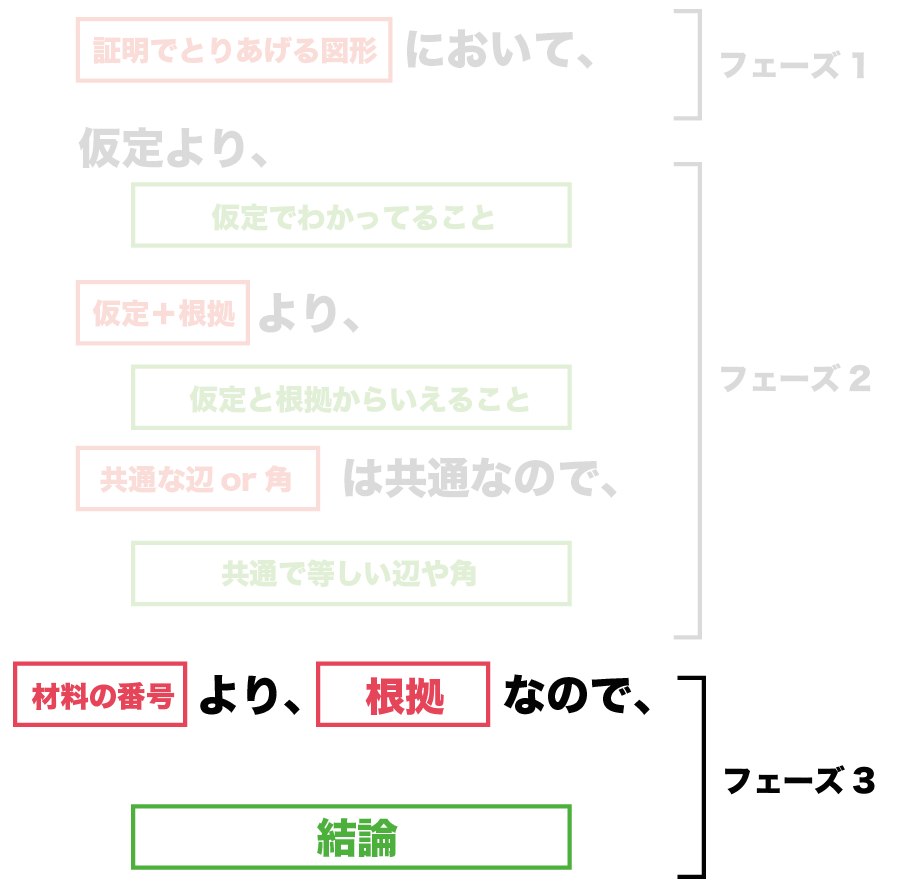



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく
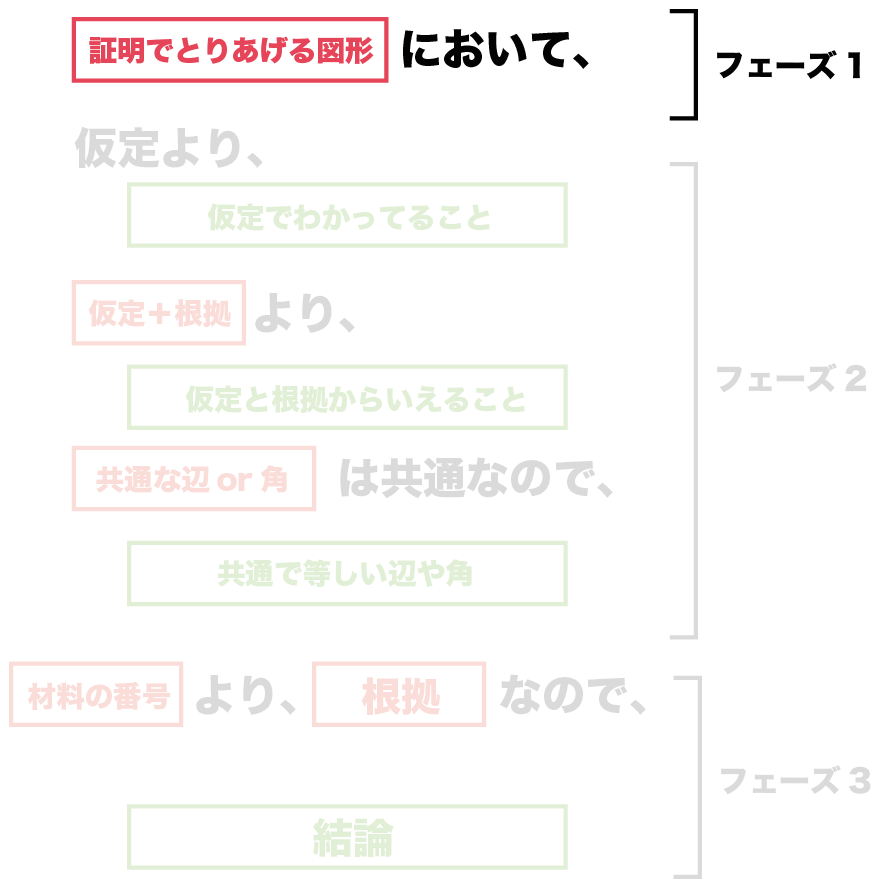



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




三角形の合同証明の進め方 中2数学 Youtube



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
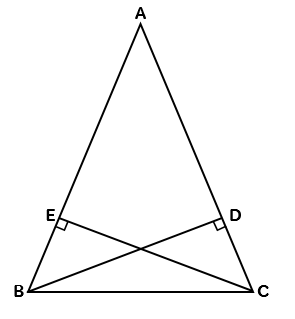



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
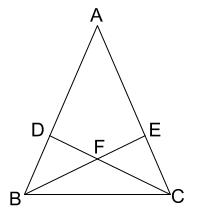



中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su



3




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張




中2数学 証明とは 例題編 映像授業のtry It トライイット




中学数学 証明 証明が苦手な中学生さんへ 家庭教師が教えるコツとポイント 新潟の家庭教師 ホームティーチャーズ




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon



この問題の証明の書き方を教えてください 錯覚が等しいため 二 Yahoo 知恵袋




中2数学 証明はハンバーガーだ2 中身の書き方のコツ 練習編 映像授業のtry It トライイット




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
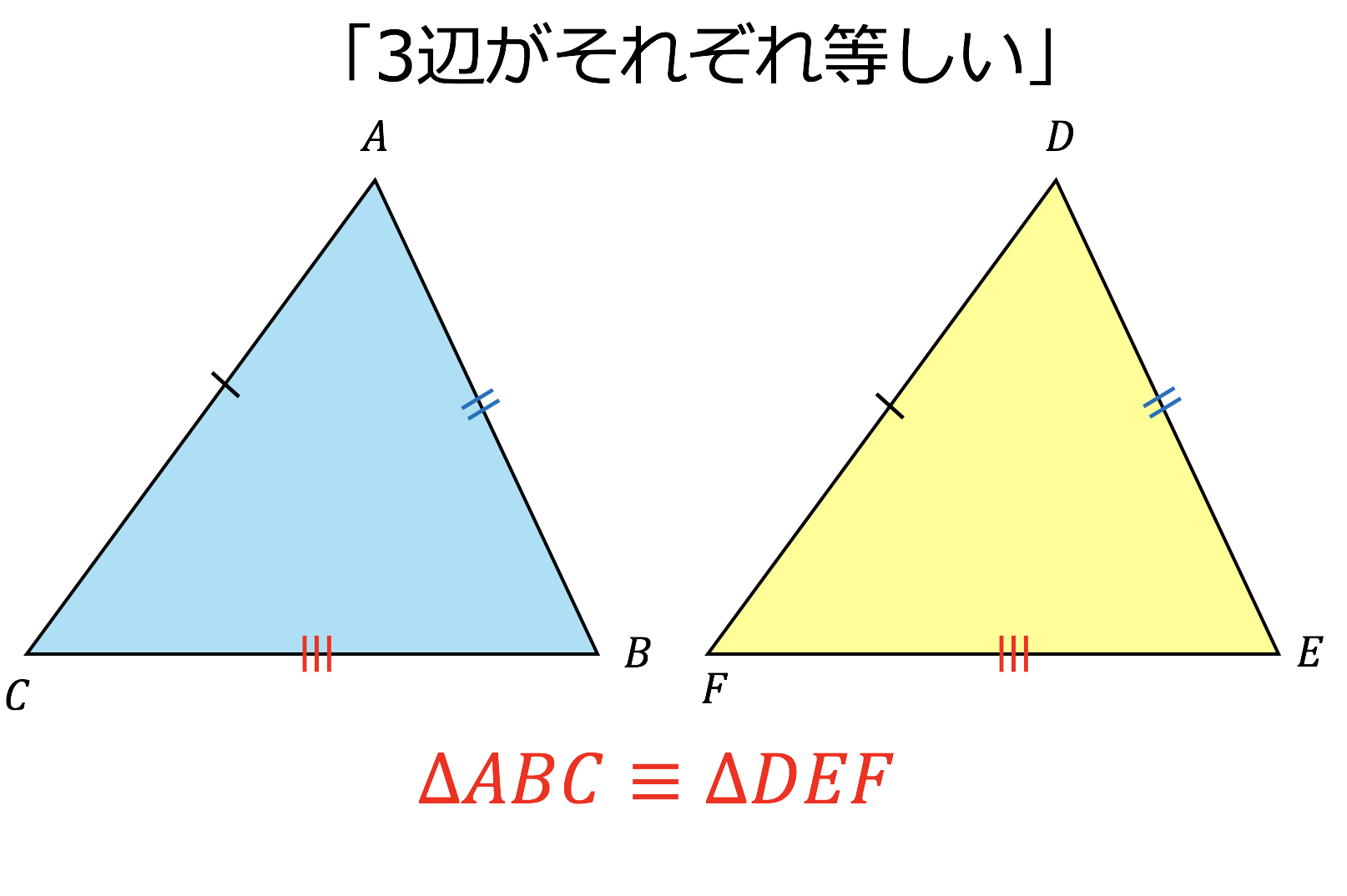



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ
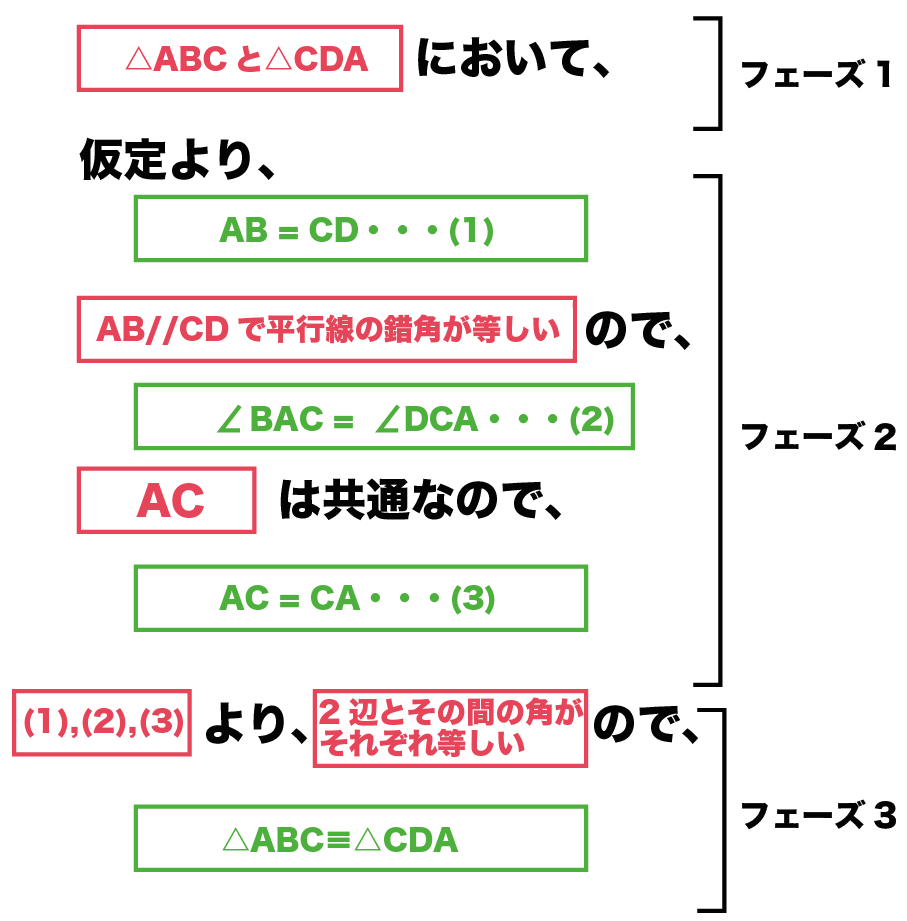



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく
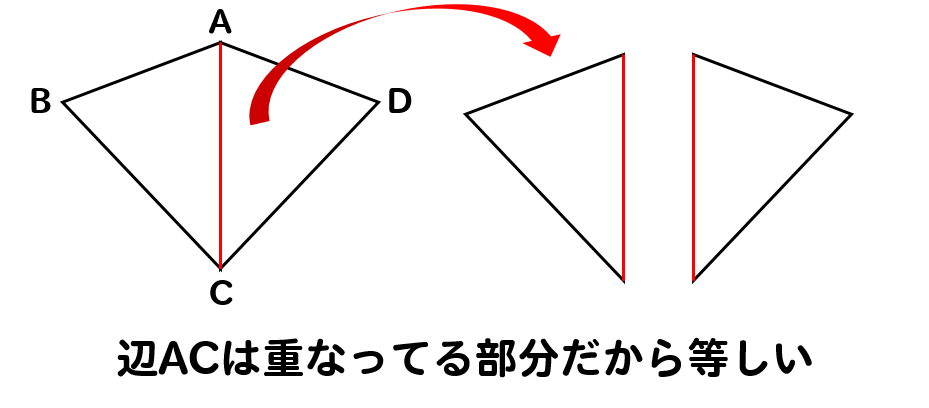



証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




対頂角が等しいと証明したいのですが この書き方は正しくないのでしょうか Clear
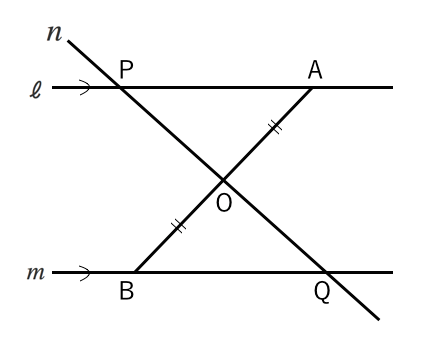



合同な図形 三角形の証明問題 苦手な数学を簡単に




二等辺三角形になることの証明 Youtube
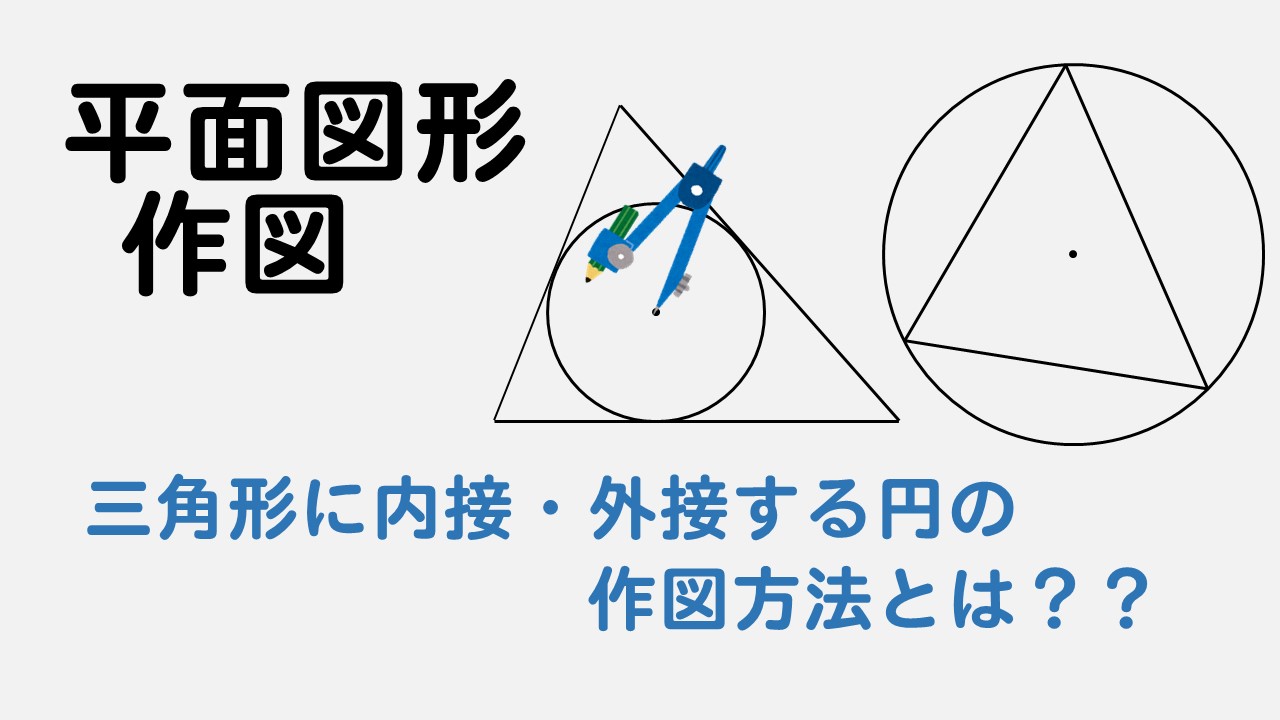



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ
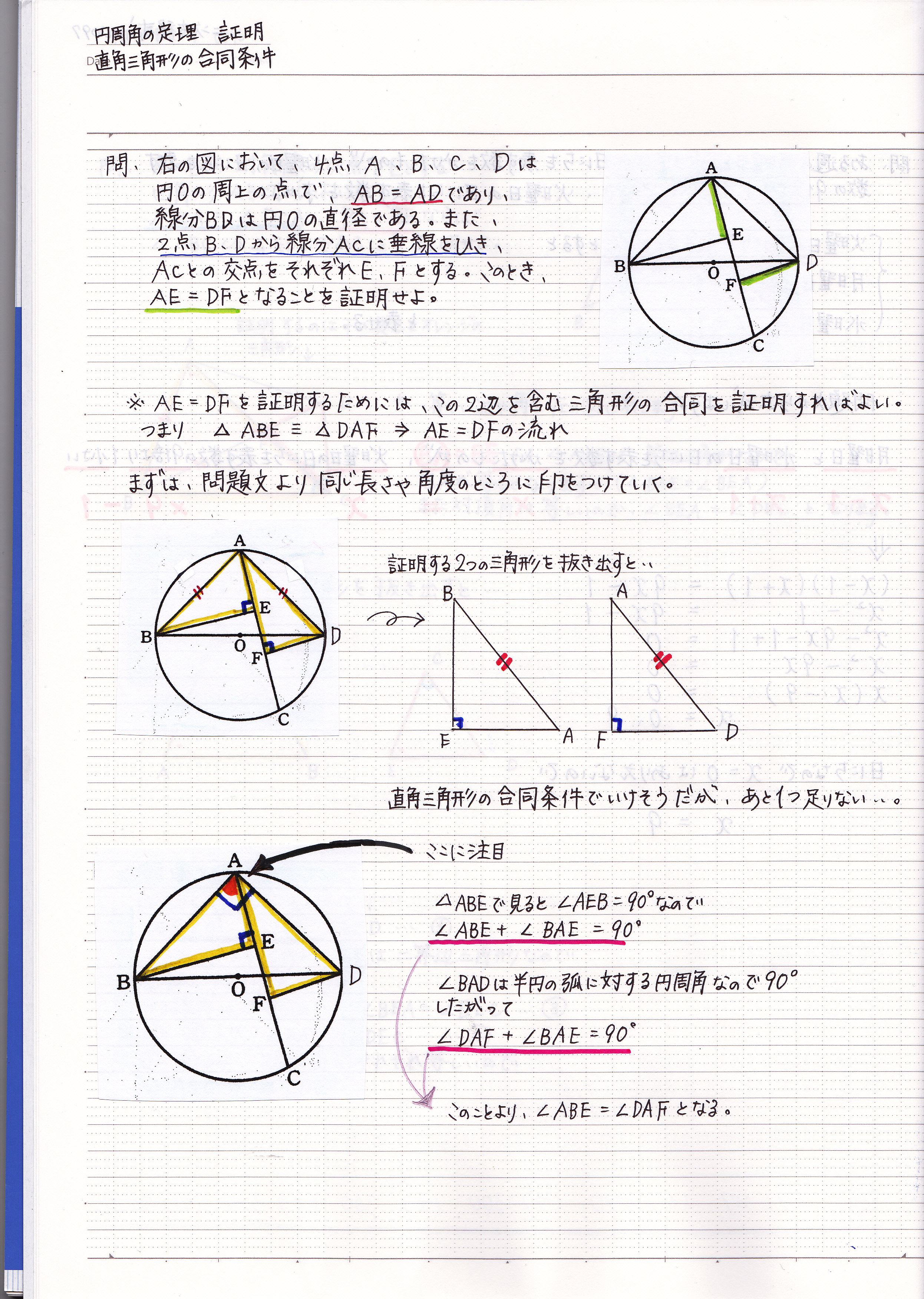



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方



角の二等分線 の作図方法 コンパス 定規 数学fun



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく



中2 数学 中2 60 証明のしくみ Youtube
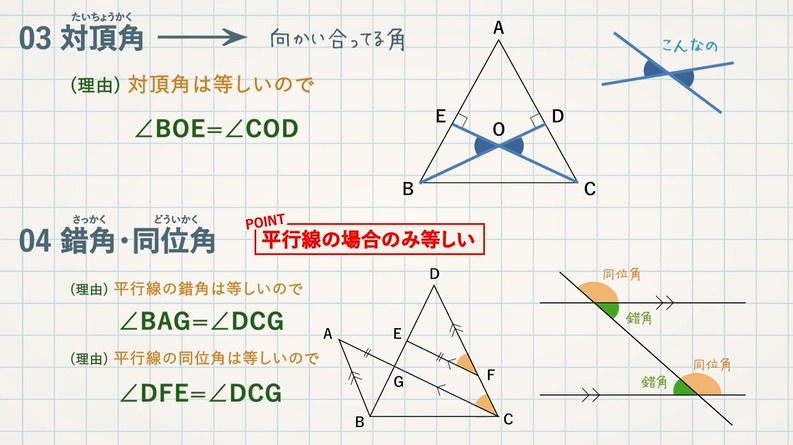



証明 合同 相似 が苦手な人へ 教遊者



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく



三角形の合同の証明の書き方




三角形の合同証明の練習 無料で使える中学学習プリント



三角形の合同の証明問題 中学 時空先生のドリルプリント



Mathematics 二等辺三角形 二等辺三角形になることの証明 働きアリ




証明 合同 相似 が苦手な人へ 教遊者



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典




証明問題です 書き方がわからないです これで合ってますかね Clear




合同な図形 正三角形の証明問題 苦手な数学を簡単に



1




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




中2数学 角度や辺が等しいことを証明する問題 例題編 映像授業のtry It トライイット



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
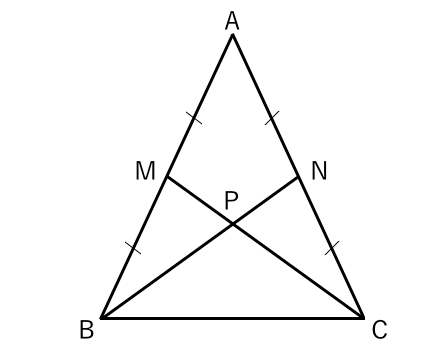



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル




高校数学a 三角形の五心 三角形の傍心とその存在証明 受験の月
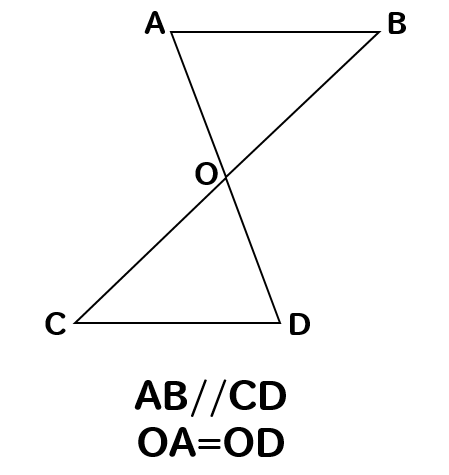



証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ
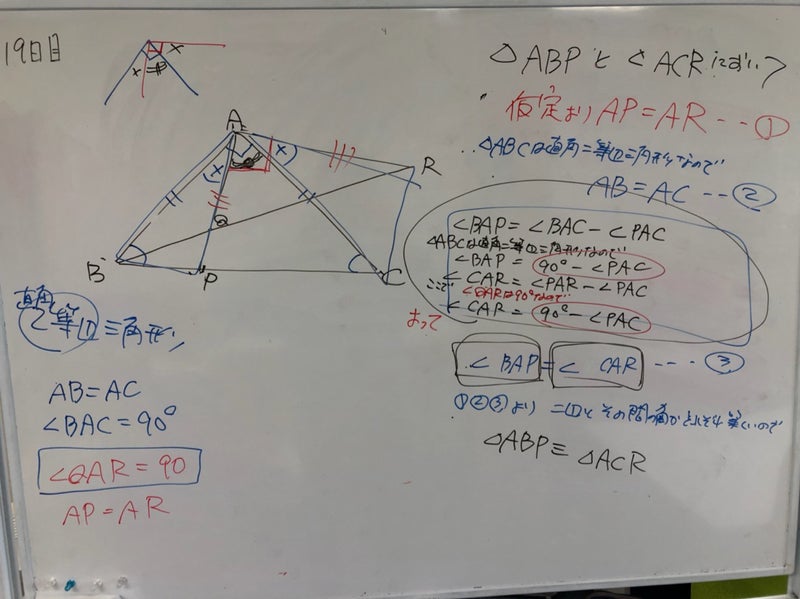



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath
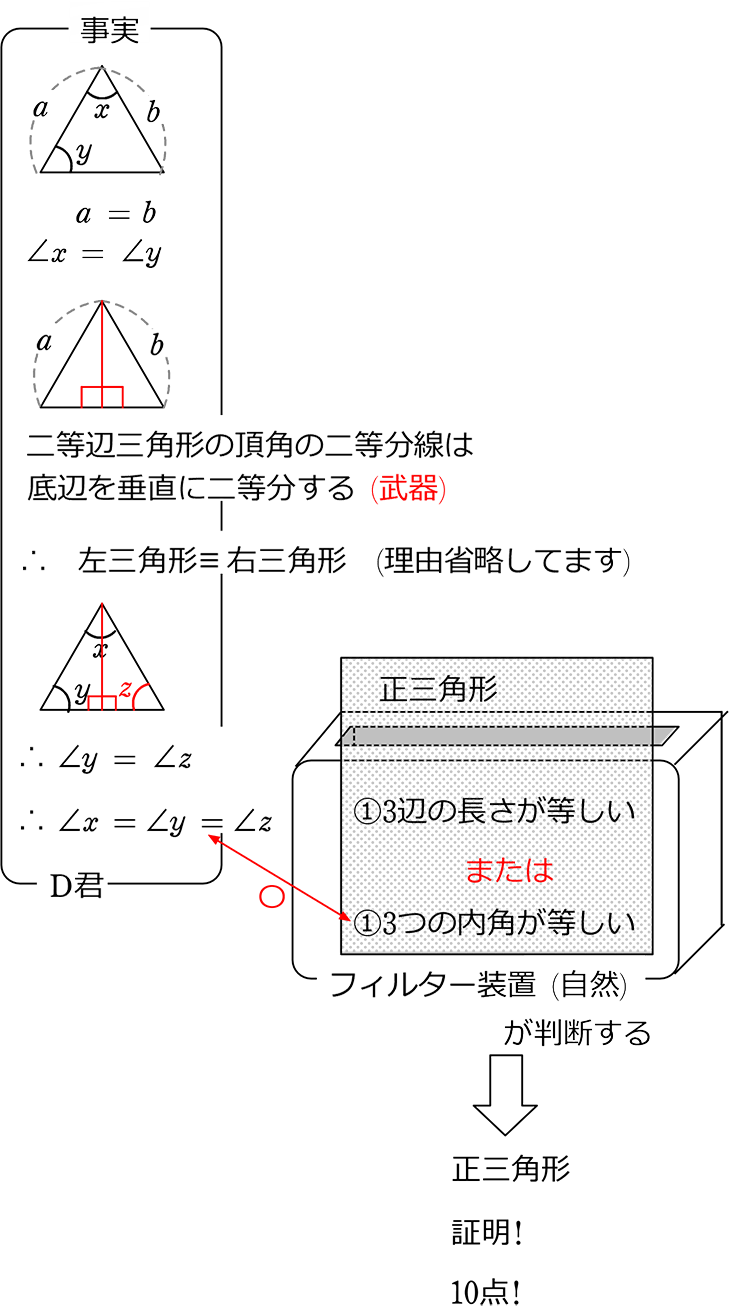



中学数学 図形の合同 図形の性質



Yebiqklp1db Pm




証明 合同 相似 が苦手な人へ 教遊者




数学 中3 46 相似の証明チャレンジ Lv 1 Youtube



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ




この書き方以外の証明の仕方ないでしょうか Clear



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




二等辺三角形と証明 Youtube



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく
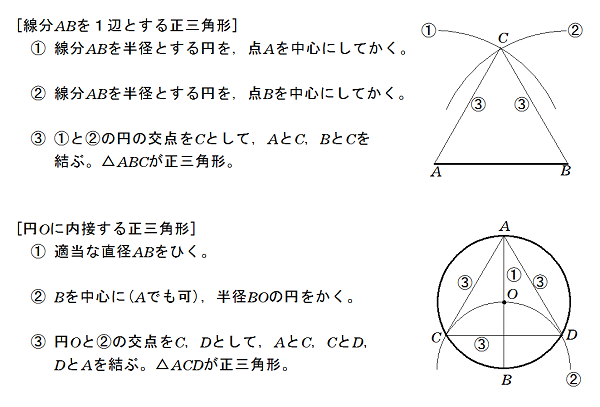



三角形と四角形 正三角形の作図のしかた 中学数学 定期テスト対策サイト



Wordで使える 二等辺三角形の合同の証明の図 Wordで数学問題プリントを作ろう




証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ



Studydoctor作図の証明 中2数学 Studydoctor




直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
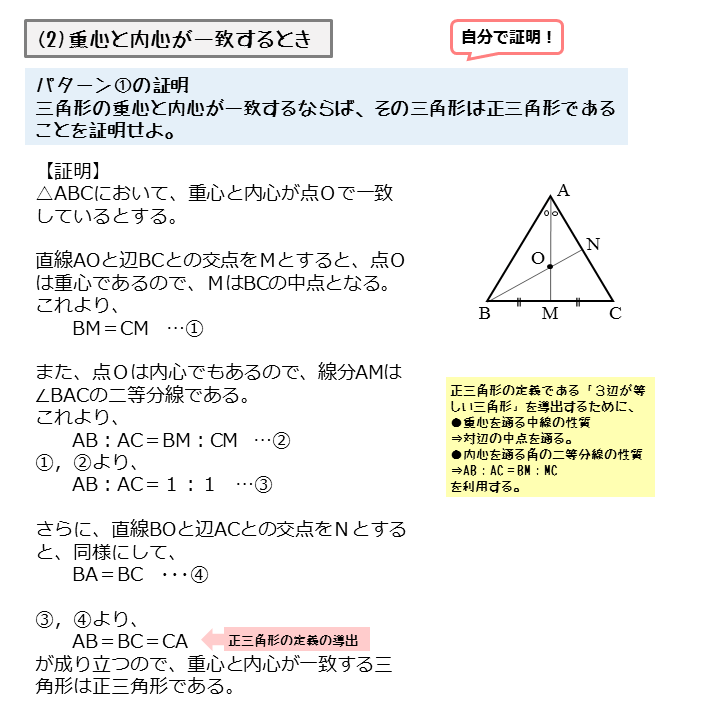



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath




二等辺三角形と証明 Youtube
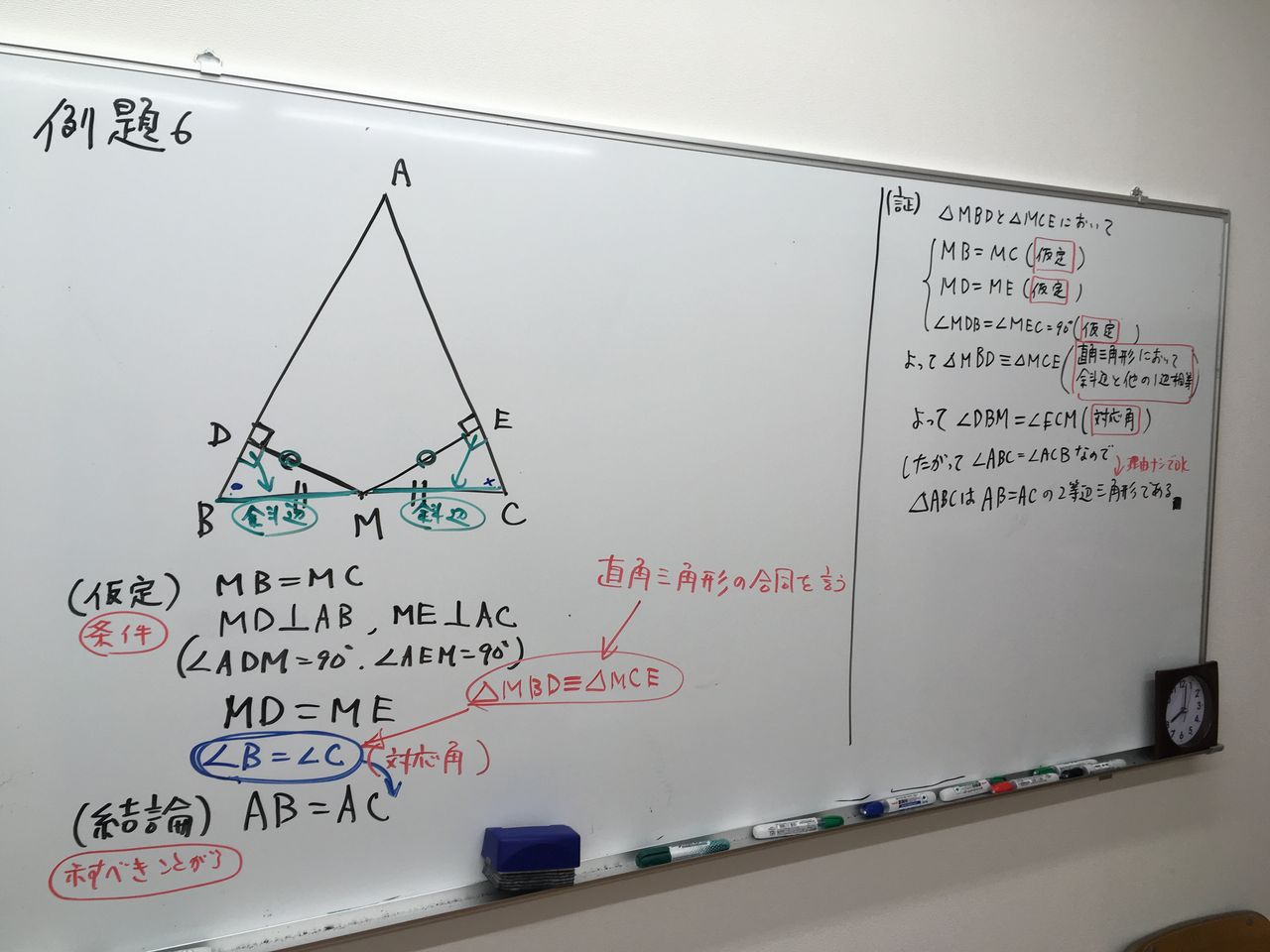



証明の書き方の作法を身につける 思考研のブログです
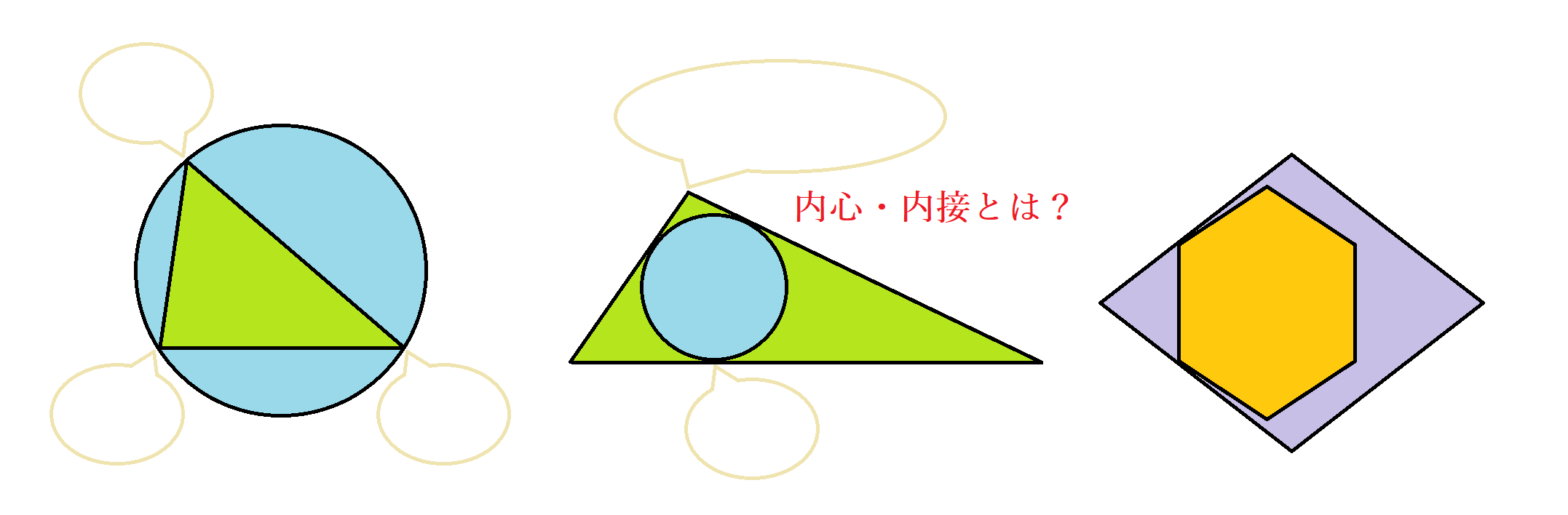



数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog




三角形の合同条件と証明問題の解き方 数学fun



内接円 内心
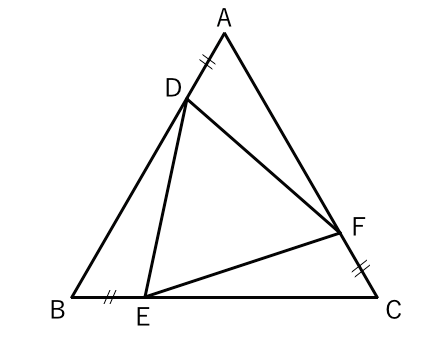



合同な図形 正三角形の証明問題 苦手な数学を簡単に




相似の証明 チーム エン




三角形の合同証明の練習 無料で使える中学学習プリント
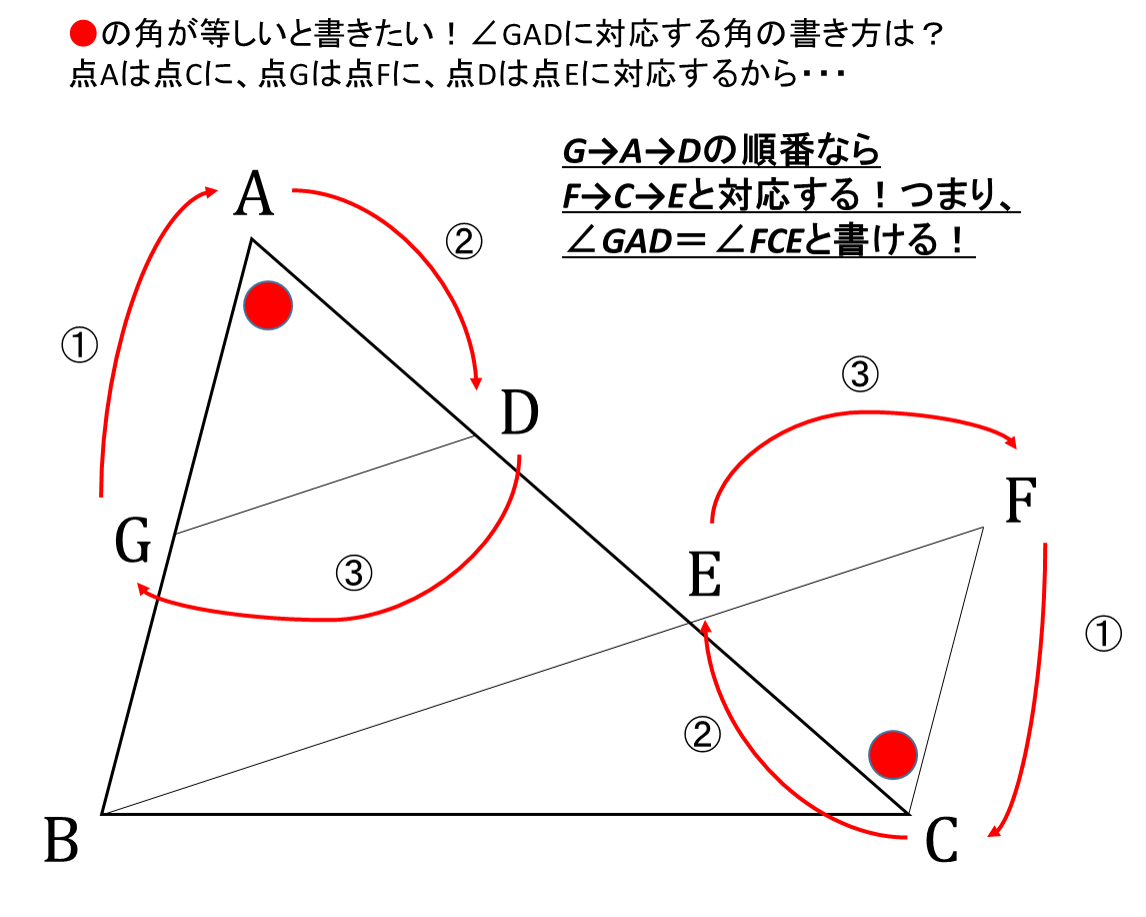



数学 中学証明問題を解く4つのポイント
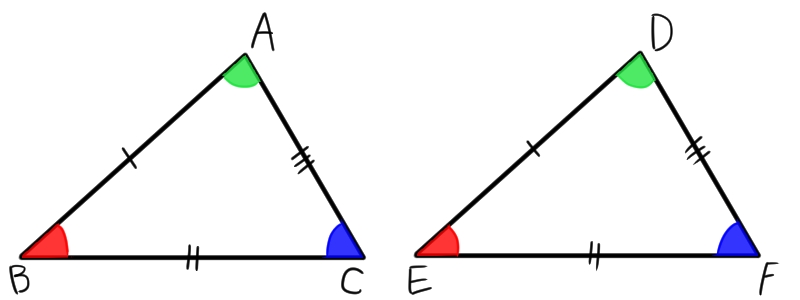



中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath




中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath
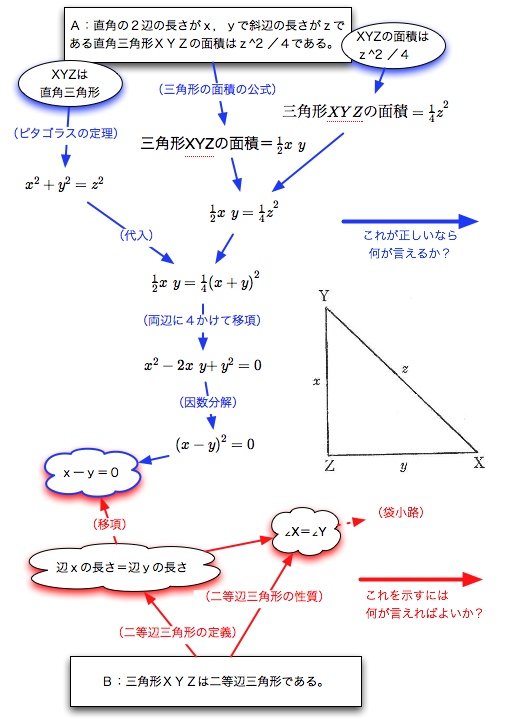



それでも証明が書けないあなたのためにテンプレートを提供しようー数学となら できること 読書猿classic Between Beyond Readers



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
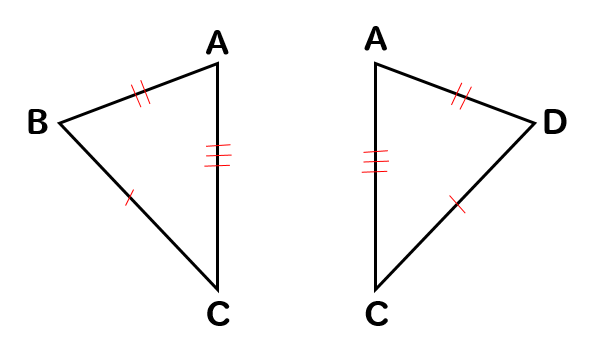



証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ



中2期末 数学 加茂ゼミナールのブログ
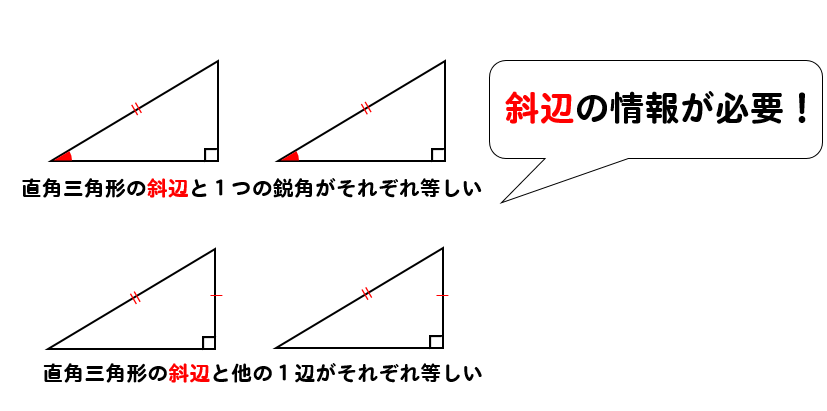



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
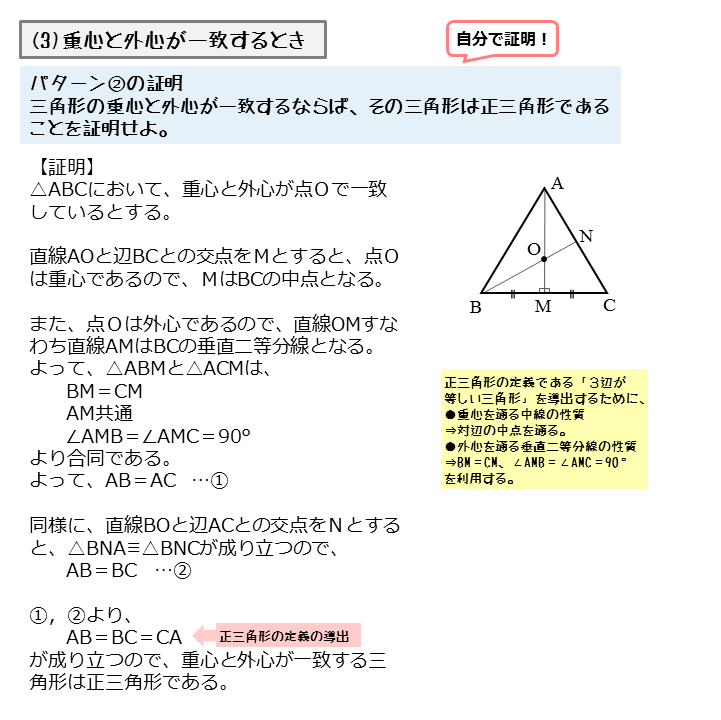



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
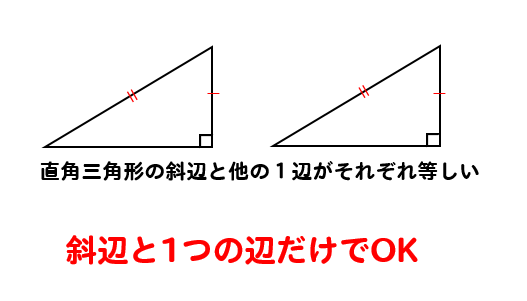



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




中2 三角形の合同を利用した証明問題 基本編 これで基礎バッチリ 中学生 Clear



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ



0 件のコメント:
コメントを投稿